五子棋智能博弈算法研究与实现

郑健磊，匡芳君

（温州商学院 信息工程学院，浙江 温州 325035）

 

摘  要：针对五子棋棋型的定义不准确，棋型不充足等问题，提出了一套改进的五子棋棋型模型和估值方法。然后针对利用极小极大值搜索和Alpha Beta剪枝算法对此棋型模型着棋时存在效率低和博弈水平不高的问题，提出了一系列改进的着棋方法，即利用局部搜索、多线程技术、浅层最优算法优化剪枝算法，以提升着棋的速度和准确率。实验结果表明，提出的着棋方案能提升着棋效率和准确性，设计得出的五子棋博弈系统具备比远超过多数人类玩家的棋力。

关键词：五子棋；估值函数；Alpha-Beta搜索算法；局部搜索；多线程

中图分类号：TP301.6         文献标识码：A

 

基金项目：国家自然科学基金项目（61402227）

作者简介：郑健磊（1996.10-），男，浙江省绍兴人，本科生，主要研究方向为智能算法与软件开发等。联系电话：13968869792，E-mail：zh_jl@qq.com；匡芳君(1976.10-)，通信作者，女，湖南衡阳人，教授，博士，从事群智能与多目标优化、模式识别与数据分析、信息安全等研究。联系电话：15988761189。

 

Design and implementation of intelligent game algorithm for Gobang

ZHENG Jian-lei，KUANG Fang-jun

School of information engineering, Wenzhou Business College, Wenzhou 325035

Abstract: Proposes a set of improved Gobang chess patterns and valuation methods for the problems of inaccurate definition of Gobang chess patterns and inadequate chess patterns. Then, for the problems of low efficiency and low game level when using the Minimax search algorithm and Alpha Beta pruning algorithm in this game model game, a series of improved game methods are proposed, namely, using local search, multithreading technology, the shallow optimal algorithm optimizes the pruning algorithm to improve the speed and accuracy of the game. The experimental results show that the proposed game scheme can improve the efficiency and accuracy of the game, The resulting Gobang game system has more than a majority of human players.

Keywords: Gobang; valuation function; Alpha-Beta search algorithm; local search; multithreading

 

1     引言

五子棋是一款经典的两人对弈的纯策略型棋类游戏。相对于国际象棋，中国象棋，围棋，日本将棋，五子棋简单易学，但是精通五子棋并非易事。2016年，AlphaGo，击败人类围棋冠军李世石^[1]，计算机在围棋领域不可能战胜人类的预言破灭。虽然AlphaGo已经宣布退出围棋比赛，但是其留下来的宝贵算法和围棋招数是计算机界的新突破，也给围棋界带来翻天覆地的变化。在五子棋领域，五子棋先后于1994年^[2]、2001年^[3]被计算机证明原始无禁手、原始有禁手规则下先手必胜，然而，相比计算机象棋和围棋，计算机五子棋的发展是缓慢的。很多五子棋专家相信目前的五子棋程序依旧无法超越最强的人类棋手。

五子棋博弈研究学者们都其独到见解，如：张明亮^[4]通过各类棋型估值的研究，优化了五子棋估值函数，解决了部分五子棋程序估值不完善的问题；毛丽民等^[5]结合图像采集和分析,研发可以进行实物对弈的五子棋机器人；程宇等^[6]通过对Alpha Beta剪枝算法的改进，优化了着棋效率低下的问题；还有学者设计和实现了整套完整的五子棋人机博弈软件^[7-8]。但五子棋博弈系统仍然存在棋型定义模糊，说法不一和博弈水平不高等问题。因此，本文针对五子棋棋型的定义不准确，棋型不充足，提出一套改进的五子棋棋型模型和估值方法，对基本棋型和绝杀棋型分别进行估值；针对Alpha Beta剪枝算法存在效率低和博弈水平不高等问题，提出改进智能博弈算法，利用多线程技术和浅层最优算法优化Alpha Beta剪枝算法，以提升着棋速度和准确率，通过局部搜索，加深程序的局部观，使得系统着棋能力得到提升。

2     五子棋棋型与估值

五子棋棋型存在定义模糊，如对活二、眠三、死四定义的不完整或存在术语使用不当^[9]。而在大部分论文中，考虑的棋型较少，如对活三的定义不够完整，对跳活三，跳四这样的重要棋型未进行定义或定义不完整^[10]。本文对棋型进行新的定义，特别是对一些特殊绝杀棋型进行了直接定义，以降低搜索深度，即颠覆从前往后的计算方式，直接从后往前推算，可提供接近2层的计算深度，而庞大的搜索树需要提高1层的搜索深度也是非常不容易的。

2.1五子棋的基本棋型

在五子棋博弈中，活三和冲四是五子棋着棋过程最重要的棋型，活三两头均可进攻，冲四具有绝对先手，连续的冲四和活三的进攻是五子棋获胜的关键技术。而活三的一些变体棋型，如有一边空一格被对方棋子拦住，如图1的棋型g所示。此外跳活三，跳四，也是十分重要的棋型。跳四和冲四一样，具备绝对先手。

2.2五子棋的绝杀棋型

如果不考虑是因为对手没有发现，而使得当前棋局存在下一着可以形成活四或者成五的情况。那么活四或者成五一定是由多个棋型连续进攻所形成。本文例举了一方因无法防御而导致另一方必定出现活四或成五的棋型如图1所示，因此着此类棋型是获胜的关键所在。通过棋型可以判断，此类棋型是由两个或两个以上的先手棋型组成。因此本文将先手棋型进行计数，如果一方先手棋型的数量超过2个，那么就给予一个相对非常高的分值，这些先手棋型包括，活三，跳活三，冲四，跳四。在着棋过程中发现，绝杀棋型有时也会存在被对手反胜或者化解的情况，这一般是因为对方连续着绝对先手棋型，即冲四或跳四，而导致的。而绝杀棋型中存在绝对先手的棋型，则不会存在此类情况，相对胜率会更高。

    

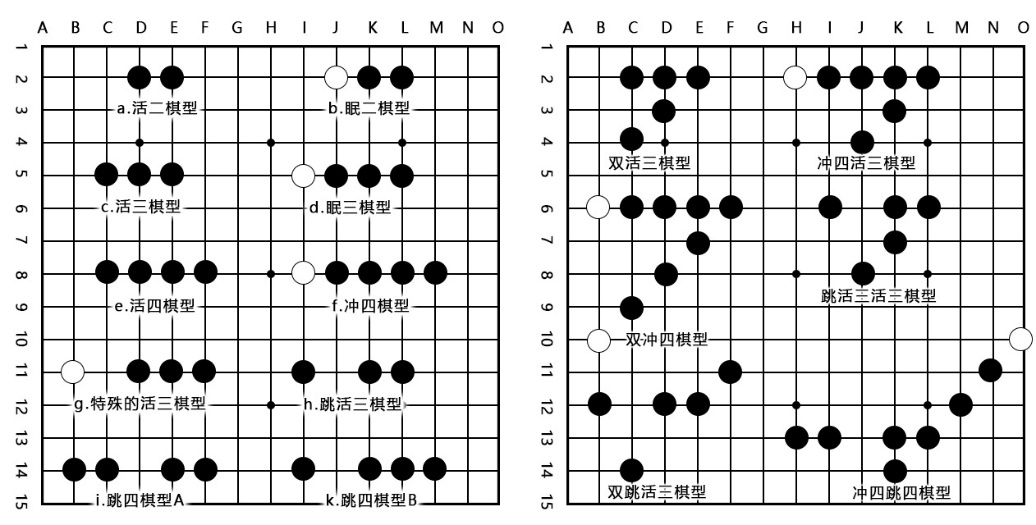
图1 五子棋主要棋型与部分绝杀棋型

2.3棋型的估值

通过对比不同的估值的对局胜率，以及文中对棋型的分析，最终得出表1所示估值方案。

表1 棋型估值

3     五子棋基础算法分析

3.1极大极小值算法效率分析

基于本文棋型的估值，使用极大极小值算法对局面进行评估。极大值极小值算法能够模拟人的思维，找出局面范围内最优的解。在对弈中，对局面进行评估，估值越大表明对当前棋手越有利，估分越小则表明越不利。对所有节点进行计算局面评估，其所得最高分，即所达深度所能走出的最佳棋面，记录第1手着棋位置，即是当前局面最佳着棋点。

如果不对极大极小值加以优化，这样的全盘遍历的方法会搜索大量毫无意义的点，对代码测试可以得出，在可以接受的时间内，只能进行两层搜索，即黑白各一手棋，而专业棋手能对未来十几步棋进行预测。

3.2 Alpha Beta剪枝算法效率分析

Alpha Beta剪枝算法在棋类博弈的应用也不乏优秀的研究^[11]。人类棋手在着棋的过程中不会去考虑对己方明显不利的点，和对对方明显有利的点。Alpha Beta剪枝算法就是不对那些双方都不会考虑的点进行剪枝，不进行下一步的考虑，以此将搜索树加以修剪。1975年，Knuth等证明在搜索节点排列为理想的情况下，将节点分支数记为b，深度记为d，搜索的节点数n为：

当d为偶数：  ；当d为奇数：

Alpha Beta剪枝算法高度依赖于节点的排列顺序，如果每次总是找到最差的节点，那么相当于剪枝永远不会发生，其效果相当于没有使用剪枝算法，即 。Alpha Beta 剪枝算法效率分析如表2所示，从表2可知：虽然使用Alpha beta剪枝对着棋能力有较大提升，但是其效率与理想排列状态相差甚远。

表2 Alpha Beta 剪枝算法效率分析

4     五子棋博弈算法研究与效率改进

通过对五子棋基础算法的分析，算法所存在的问题已然暴露。在极大极小值算法暴力搜索的基础上，使用Alpha Beta剪枝算法进行改进，但其效率依旧低下，且只能对第四层进行非常缓慢的搜索，因此，结合局部搜索、多线程技术和浅层最优算法提出效率改进方案。

4.1局部搜索

在五子棋博弈过程中，没有哪个人类棋手会对整个棋盘进行计算。其思考过程往往是从中心向四周发散。并且五子棋着棋往往不会超出原有棋子两格的位置。而未经优化的搜索算法会将任何一个空白的节点均作为可能的落子点。

经过文献资料和实战分析，一般对于搜索区域限制的算法往往是计算具有最大横坐标的棋子(maxx)，具有最小横坐标的棋子(minx)，具有最大纵坐标的棋子(maxy)，具有最小纵坐标的棋子(miny)，得出一个区域为(maxx- minx + n) * (maxy-miny + n)，其中n表示偏移量，即可能的着棋点和原有棋子的最大距离^[6]，但是这的计算方式并不高效。如果棋型呈现斜向狭长走势，或者棋子距离较远中间有大量空白的情况，依旧会存在大量的无效搜索，而且前者的情况并不少见，且在五子棋博弈过程中，与任何已有棋子成不了直线的点也往往是不会成为落子区域，这样就会出现如图2所示的区域化限制着棋点潜在的缺陷。对此，本文提出一种新思路，计算所需搜索节点的坐标，即可精确确定搜索范围。这样记录节点坐标的计算方式虽然比记录搜索范围计算方式更加复杂，但其减少的时间依旧比其增加的时间更可观。

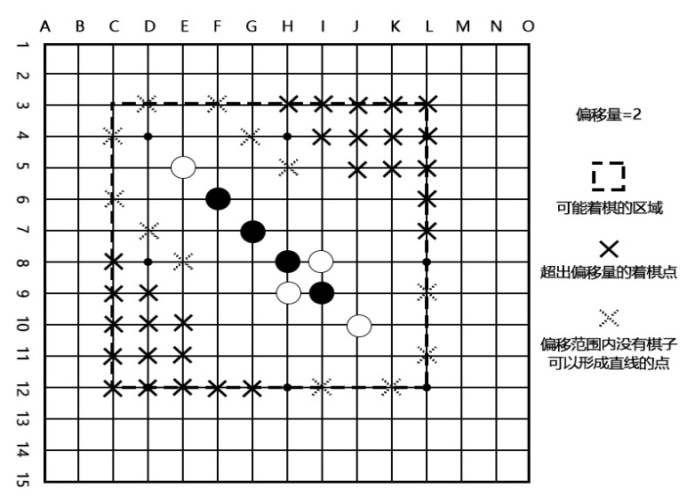
图2 区域化限制着棋点潜在的缺陷

本文局部搜索使用偏移量为2，其伪代码如下：

for (遍历整个棋盘) {

if 当前节点存在棋子

       for 对当前偏移量为1的范围内进行搜索 {

       if 当前节点没有棋子，且当前节点未被记录

              then 记录当前节点坐标，并将当前节点记为已记录

       endif

}

              endif

if 当前节点存在棋子

       for 对当前偏移量为2的范围内进行搜索 {

       if 当前节点没有棋子，且当前节点未被记录，且横纵偏移量相等

              then 记录当前节点坐标，并将当前节点记为已记录

       endif

}

              endif

}

使用局部搜索前后的节点量对比如表3所示，局部搜索效果非常有效，第二层和第四层节点分别减少了97.87%和99.92%，且原本无法计算的第六层使用较长时间也可被成功计算。

表3 使用局部搜索前后的节点量对比

4.2多线程技术

使用局部搜索之后，搜索速度有了质的飞跃。但博弈的程中又出现了新问题，即在4层和6层搜索的过程中CPU 的平均占用率只有35%左右。研究后发现，这是因为整个搜索的过程是单线程串行的，而现在的CPU普遍采用了多核多线程设计，实验所用的笔记本电脑使用的是Intel i7 8550U处理器，使用了4核8线程的设计。多线程技术避免了因阻塞带来的等待问题，能够有效提高处理器的工作效率和资源利用率。^[12]。

本文采取了多线程技术来优化CPU 的使用率，目前市面上多数消费级CPU采用的是2核4线程，4核4线程，或者4核8线程的设计。因此，选择了4线程对搜索进行优化。

本文通过给每个线程分配不同的搜索区域，达到四线程搜索，其伪代码如下：

length=搜索数组的长度;

range1[开始] = 1;  range1[结束] = length / 4;

range2[开始] = range1[结束] + 1;  range2[结束] = length / 2;

range3[开始] = range2[结束] + 1;  range3[结束] = (range2[结束] + 1 + length) / 2;

range4[开始] = range3[结束] + 1;  range4[结束] = length;

通过将局部搜索时保存的节点数组4等分，然后使用4个线程分别对4个节点数组分别进行搜索。改进后CPU占用率从35%左右提升到了95%左右，而剩下的5%也已经被其他任务占据，因此CPU的使用率已经达到了100%。

4.2.1效率分析

CPU效率得到明显提升，本应该计算速度也明显提升。但是实验结果却是令人意外的，实验多线程搜索之后，节点数几乎是使用单线程的2~3倍。单位时间内对节点的搜索速度提高到了原来的2倍左右，如表4所示，反而需要比单线程更长的时间。而且多线程的博弈过程发现，当前局面存在冲四棋型时，个别线程的节点明显增多。

表4 使用多线程技术前后的节点量与时间（取前10次平均值）对比

4.2.1多线程效率低下的原因分析

经过多次博弈发现，多线程效率低下是因为四个线程彼此独立，个别线程所找到着棋点有时候往往是非常不好的，导致个别线程剪枝不易发生。最为显著的是出现浅层绝杀的棋面，如对方着棋形成了冲四，那么只有一个线程可以找到拦截冲四继续形成成五的点，而其他线程因为这个点不在它的搜索范围内，导致得到的永远是一个极差的局面分。

如果使用单线程，那么单棵的搜索树将被分成4棵彼此独立的搜索树，虽然4线程的每棵小树的节点比单线程的大树要更少，但是4棵树的总和却要更多。而多线程并不能带来4倍的速度提升，因为CPU负载升高后其每个线程所获得的算力明显低于单线程。

4.3浅层最优算法

Alpha Beta剪枝算法严重依赖于节点的排列。如果程序总是先去搜索最坏的节点，那么Alpha Beta截断就不会发生，该算法最终会遍历整个搜索树。在搜索的过程中，节点的排列顺序是完全无规律的，甚至没有优化的搜索往往是从边缘往中心推进，这样得到的节点往往比随机排列还要更差。显然找到最优排列是不可能的，因为这势必要算出所有节点。但是可以通过着棋的特点，算法的特性，提前找到较为优秀的解。

浅层搜索虽然不能找到深层的最优解，但是其找到的解往往是较优解。而且对于某些棋型，浅层的搜索结果和深层的结果是完全一样的。比如下一着如果可以形成活四，那么不管搜索深度是多少，着活四棋型永远都是最优解。通过这一特点，在原来的Alpha Beta剪枝算法的搜索范围的基础上，先使用两层搜索找到一个当前局面的最优解，再将这个解的节点替换为深层搜索的每一个线程的起始节点，那么深层搜索将从一个较为优秀的节点开始搜索。浅层最优搜索算法的伪代码如下：

(x,y)=获取深度为2的最佳着棋点;

线程1计算范围[0][0]=x; 线程1计算范围[0][1]=y;

线程2计算范围[0][0]=x; 线程2计算范围[0][1]=y;

线程3计算范围[0][0]=x; 线程3计算范围[0][1]=y;

线程4计算范围[0][0]=x; 线程4计算范围[0][1]=y;

这样算法将四个线程都能联系，尤其是在浅层绝杀的棋面下，让四个线程都有机会找到绝杀点，大大提高了搜索效率，如表5所示，使用了浅层最优算法后的多线程搜索效率显著提高。浅层最优算法不仅解决某些线程因找不到拦截浅层绝杀的点而导致搜索速度极慢，还使得节点排列顺序有一定提升，如表6所示，单线程也比不使用浅层最优算法的效率高。

表5 使用浅层最优算法前后多线程的节点量与时间(取前10次平均值)对比

 

表6 使用浅层最优算法前后单线程的节点量与时间(取前10次平均值)对比

使用了浅层最优算法之后，无论单线程与多线程都有了效率的提升，使用浅层最优算法后单线程与多线程的节点量与时间对比如表7所示。

表7 使用浅层最优算法后单线程与多线程的节点量与时间对比

由表7可知，在节点多的时候，多线程表现出的效率要优于单线程，而在节点较少的时候，单线程效率更优。由于深度为2的时候，无论基于什么算法，都是瞬间完成的，因此不在考虑之内。对于深度4和深度6而言，多线程的综合速度要明显优于单线程，随着棋面复杂度的增加，搜索深度加深，多线程的优势将更加明显，因此多线程的表现是值得肯定的。

5     实验结果与分析

全文实验方式均采用了15x15的标准五子棋棋盘，以前10步着棋为实验数据，并保持相同深度的着棋棋型一致，对所使用的各项技术进行分析。通过使用五子棋基本棋型和绝杀棋型的两种估值方式，对棋力带来了明显改善，尤其是对于浅层绝杀方面。对于极大极小值算法和Alpha Beta剪枝算法效率不足的问题，提出了以下改进方案：

（1）局部搜索意在优化减少对理论上不会落子的区域进行优化，并且本文打破常见的计算着棋区域的方法，转而使用了直接计算落子坐标的方法，优化了前者所存在的不足，其效率提升也十分明显，带来约99%的综合效率提升，并使得6层搜索成为了可能。

（2）对CPU使用率过低的问题，采取了4线程并行计算，但是其结果并不理想，因为Alpha Beta剪枝算法的特点，其效率反而有所下降。

（3）为了解决多线程计算存在的问题，提出了浅层最优算法，此算法不仅提高了多线程效率，也提高了单线程效率，使用了浅层最优算法之后，效率较低的多线程搜索有了较大的改善，相对于未使用此算法提升了约60%的综合效率。

如图3是系统程序对局测试的结果，玩家持黑，电脑持白，电脑从第13手进行了连续的先手进攻，最终于第27手取胜。

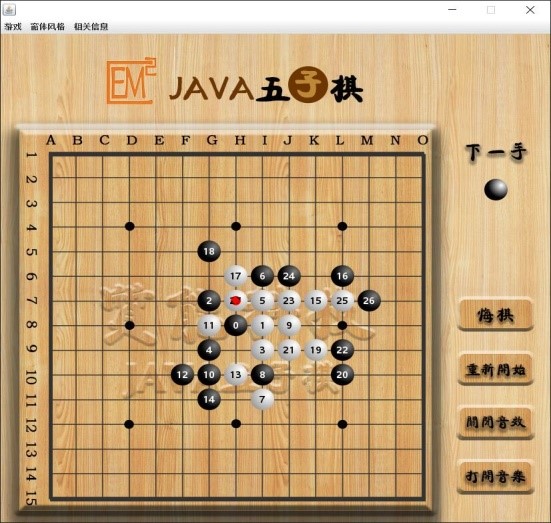
图3 电脑持白对弈过程

6     结束语

本文针对五子棋棋型的定义不准确，棋型不充足等问题，提出了一套改进的五子棋棋型模型和估值方法。针对利用极小极大值搜索和Alpha Beta剪枝算法对此棋型模型着棋时存在效率低和博弈水平不高的问题，提出改进智能博弈算法，在可接受的时间内，将搜索深度做到了6层，实验结果表明，程序性能和效率相对较高，通过使用五子棋基本棋型和绝杀棋型的两种估值方式，对棋力也有明显改善，尤其是浅层绝杀方面有着很大优势。下一步工作将使用机器学习算法保存已下棋局，以使同样错误的着棋不再出现，同时在着棋时考虑对手存在计算漏洞，使程序具备更激进棋风。

参考文献

[1]麦柯. 从人机大战到机机大战，AlphaGo Zero颠覆的不仅仅是围棋[N].电脑报,2017

[2] Allis L V. Searching for Solutions in Games and Artificial Intelligence[D]. Ph D Thesis, 1994.

[3] Wágner J, Virág I. Solving Renju[J]. Icga Journal, 2001, 24(1):30-34.

[4] 张明亮, 吴俊, 李凡长. 五子棋机器博弈系统评估函数的设计[J]. 计算机应用, 2012, 32(7):1969-1972.

[5]毛丽民, 朱培逸, 卢振利,等. 基于LabVIEW的五子棋博弈算法[J]. 计算机应用, 2016, 36(6):1630-1633.

[6]程宇, 雷小锋. 五子棋中Alpha-Beta搜索算法的研究与改进[J]. 计算机工程, 2012, 38(17):186-188.

[7]张效见. 五子棋计算机博弈系统的研究与设计[D]. 安徽大学, 2017.

[8]王杨. 基于计算机博弈的五子棋算法研究[D]. 沈阳理工大学,2016.

[9]王长飞, 蔡强, 李海生. 智能五子棋算法的设计实现[J]. 系统仿真学报, 2009, 21(4):1051-1054.

[10]徐建. 五子棋的一种价值的估算[J]. 智能计算机与应用, 2016, 6(5):90-92.

[11] Sato N, Ikeda K. Three types of forward pruning techniques to apply the alpha beta algorithm to turn-based strategy games[C]. Computational Intelligence and Games. IEEE, 2017:1-8.

[12] 周佳佳, 李涛, 黄小康. 多核同时多线程处理器的线程调度器设计[J]. 电子技术应用, 2016, 42(1):19-21.